NeRF
Abstract
본 논문은 input view set을 사용하여 연속적인 volumetric scene 함수을 최적화하고 복잡한 scene의 새로운 이미지를 합성하는 sota 결과를 만들어 냈습니다. 본 논문의 알고리즘은 fully-connected deep network를 사용하는데, 5D 좌표 $(x,y,z,\theta,\phi)$의 input을 volume density와 해당 위치에서 방출하는 view-dependent한 radiance를 output으로 가집니다.
본 논문은 5D 좌표를 조회하여 v이미지를 합성하고, output color와 density를 image로 투영하는 classic volume rendering 기술을 사용합니다. volume rendering은 미분가능하기 때문에, 본 논문의 input을 최적화 하는 것은 camera pose의 image set입니다. 본 논문은 어떻게 효과적으로 neural radiance field를 최적화 하는지에 대한 방법에 대하여 묘사하고 있습니다. 또한 이전의 neural rendering과 view synthesis에 관련한 연구보다도 뛰어난 성능을 보여주고 있습니다.
Introduction
이번 연구에서는, view synthesis에서 오랜시간 해결되지 않았던 문제를 5D scene representation을 최적화하여 captured된 image set을 rendering 할때의 error를 최소화함으로 해결했습니다.

5D 좌표 $(x,y,z,\theta,\phi)$를 volume density와 view-dependent RGB color로 축약하는 함수를 표현하기 위하여 convolutional layer없는 neural network (즉, MLP)를 최적화 합니다. 이 neural radiance field (NeRF)를 render하기 위하여 몇 가지 viewpoint가 있습니다.
-
3D points의 sampled된 set을 generate하기 위하여 camera 광선을 진행시킵니다.
-
그 3D point와 대응하는 viewing direction을 neural network의 input으로 넣고, color와 density의 output set을 생성하기 위하여 neural network를 형성합니다.
-
color와 density를 축적하여 2D image로 만드는 classical volume rendering 기술을 사용합니다.
이 과정이 미분가능하기 때문에, 관찰된 image와 본 논문의 표현법으로 rendered된 view 간의 error를 최소화 하는 gradient descent를 사용하여 이 모델을 최적화 합니다. 높은 volume density와 정확한 color를 할당하여 일관성 있는 모델를 예측하기 위해, 다양한 veiw로 부터 온 error를 최소화합니다. <Fig 2>가 전체적인 pipeline입니다.
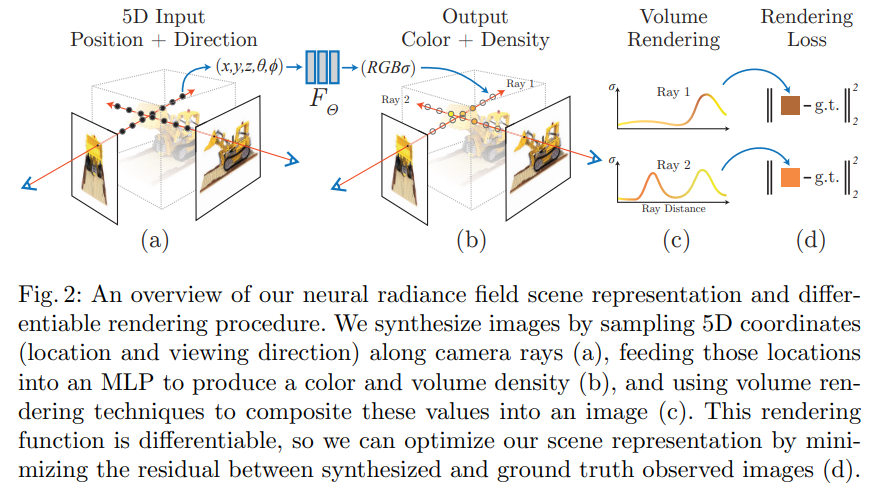
복잡한 scene을 위한 neural radiance field representation을 최적화 하는 기본적인 implementation은 충분히 고해상도를 converge하지 않고 게다가 각 camera 광선의 요구된 수가 효율적이지 않다라는 것을 알게 되었습니다. 이러한 문제를 본 논문에서는 MLP를 더 높은 frequency functions를 표현할 수 있는 MLP를 만들고 positional encoding과 함께 5D 좌표를 변환하여 해결했습니다. 그리고 계층적 sampling 절차를 사용하여 이 high-frequency scene 표현법을 적절히 sample할 수 있는 요구된 조회량을 줄였습니다.
본 논문의 방법은 volumetric 표현법의 이점을 상속받았습니다. 즉, 복잡한 real-world geometry와 appearance를 표현할 수 있으며, 투영된 image를 활용하여 gradient-based 최적화에도 적절합니다.
정리하면 아래와 같습니다.
- 본 논문의 방법은 5D neural radiance fields와 basic MLP network 파라미터화하여 복잡한 geometry와 material를 통해 연속적인 scene을 표현할 수 있습니다.
- classical volume rendering 기술을 기반으로 한 미분가능한 rendering 방법입니다. standard RGB image를 통하여 이 표현법을 최적화 할 수 있습니다. 이는 계층적 sampling 전략을 포함하여 visible scene content과 함께 space를 향한 MLP의 용량을 할당합니다.
- 5D 좌표를 더 높은 고차원의 공간으로 map하는 positional encoding을 사용합니다.
Related Work
3D spatial location을 함축된 모양의 표현법으로 변경하는 것은 computer vision에서 유망한 연구 방향입니다. 하지만 이런 방법들은 복잡한 realistic scene을 재생산할 수 없다는 문제가 있습니다. triangle mesh와 voxel grid와 같은 discrete 표현법을 사용했기 때문이죠. 두 가지 방법으로 복잡한 realistic scene을 rendering하는 기술이 있었습니다.
Neural 3D shape representations
xyz 좌표를 distnace function이나 occupancy field로 mapping하는 deep network를 최적화하여 3D shape을 함축적으로 표현하는 방법입니다.
View synthesis and image-based rendering
이미지를 합성하거나 mesh-based 표현법으로 rendering하는 방법이 있습니다.
Neural Radiance Field Scene Representation
이전과 같은 방법으로 복잡한 realistic scene을 rendering하기에는 oversmoothing된다는 단점 등이 있습니다.
본 논문은 continuous scene을 5D vector로서 나타냈습니다. 3D location $\mathbf{x}=(x,y,z)$와 2D viewing direction $(\theta,\phi)$을 가진 5D vector input을 color $\mathbf{c}=(r,g,b)$와 volume density $\sigma$의 output으로 바꿉니다. MLP network를 통하여 표현하자면 다음과 같습니다. $F_{\Theta}:(\mathbf{x},\mathbf{d})\rightarrow(\mathbf{c},\mathbf{\sigma})$ 이 식의 weight인 $\Theta$를 최적화하여 5D 좌표에 대응하는 volume density와 directional emitted color로 mapping합니다.
이와 같이 하기 위해, MLP $F_{\Theta}$는 먼저 input 3D 좌표 $\mathbf{x}$를 8개의 fully-connected layer(ReLU, 256 channels per layer)를 거쳐 output $\sigma$와 256차원의 feature vector를 만듭니다. 이 feature vector를 camera ray의 viewing direction과 concat하고 하나의 추가적인 fully-connected layer(ReLU, 128 channels)를 거쳐, view-dependent한 RGB color를 만듭니다.


Volume Rendering with Radiance Fields
$\sigma(\mathbf{x})$는 $\mathbf{x}$위치에서의 volume density를 의미하며, expected color $C(\mathbf{r})$, camera ray $\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$를 의미합니다.
함수 $T(t)$는 $t_n$에서 $t$까지의 ray의 축적된 투과율입니다. 이는 즉, 다른 입자를 치지 않고 $t_n$에서 $t$까지의 ray가 지나갈 확률을 뜻하죠. neural radiance field로부터 rendering하면 integral $C(\mathbf{r})$를 예상하는 것이 요구됩니다. 이를 통해 camera ray가 가상의 camera의 각 pixel를 통한 ray를 trace할 수 있죠.
본 논문은 quadrature를 사용하여 integral을 예측합니다. MLP는 오직 고정된 discrete한 location을 조회하기 때문에, deterministic quadrature은 효과적으로 표현법의 해상도를 제한할 수 있습니다. 대신에 본 논문은 sampling을 하여 $[t_n,t_f]$를 $N$개의 균등한 bin으로 나누고 각 bin에서 무작위로 균등하게 sample을 이끌어냅니다.
integral을 예측하기 위해 discrete한 sample set을 사용하였지만, smapling은 scene representation을 표현하도록 가능하게 만들었습니다. 몇 sample을 사용하여 $C(\mathbf{r})$를 quadrature rule로 계산하는데, 아래와 같습니다.
근접한 sample 사이의 거리는 $\delta_i = t_{i+1}-t_i$입니다.
Optimizing a Neural Radiance Field
위와 같은 식으로는 충분한 것 같지 않은 것을 발견하였습니다. 이에 본 논문은 고해상도의 복잡한 scene을 표현할 수 있도록 두 가지 성능 향상을 도입하였습니다. 첫 번째로, MLP에서 고주파수를 표현할 수 있도록 input에 positional encoding을 두었습니다. 두 번째로, 고주파수 표현법을 효과적으로 sample할 수 있도록 계층적 sampling 절차를 진행했습니다.
Positional encoding
neural network가 universal function approximators임에 불구하고, $F_{\Theta}$가 바로 $xyz\theta\phi$를 input으로 받아 rendering하면 고주파수에서 성능이 떨어진다는 것을 발견했습니다. input을 더 높은 차원으로 mapping하는데, network에 보내기전 고주파수 함수를 사용하면, 고주파수 변동을 포함한 더 적절한 data를 만들 수 있습니다.
본 논문은 이를 활용하여 두 함수 $F_{\Theta}=F_{\Theta}’\circ\gamma$로 변형했습니다. $\gamma$는 $\mathbb{R}$를 더 높은 차원 공간 $\mathbb{R}^{2L}$로 mapping하는 데에 쓰이며, $F’_{\Theta}$는 단순한 MLP입니다. encoding 식은 아래와 같습니다.
$\gamma(\dot)$ 는 $\mathbf{x}$에서 3 개의 좌표를 각각 따로 적용합니다. 실험적으로 $\gamma(\mathbf{x})$에서는 L=10, $\gamma(\mathbf{d})$에서는 L=4로 설정하였습니다. positional encoding로 불리는 Transformer의 한 구조라고 생각이 들겠지만, Transformer에서 positional encoding은 sequence에 discrete한 position을 부여하기 위하여 사용하지만, 순서에 관련된 개념은 들어가지 않습니다. 하지만 본 논문은 고차원 공간으로 input 좌표를 mapping하기 위하여 사용하기에 MLP를 좀 더 쉽게 고주파수 함수로 근사화하기 쉽습니다.
Hierarchical volume sampling
두 개의 network를 최적화 합니다. “coarse”, “fine”
sampling을 사용하여 $N_c$ 위치에서 sample을 먼저 한 다음, “coarse”를 평가합니다. 그 다음, $N_f$ 위치에서 inverse transform sampling으로 “fine”을 평가합니다.
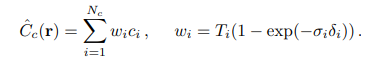
Implementation details
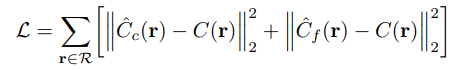
위는 loss를 구하는 식입니다.
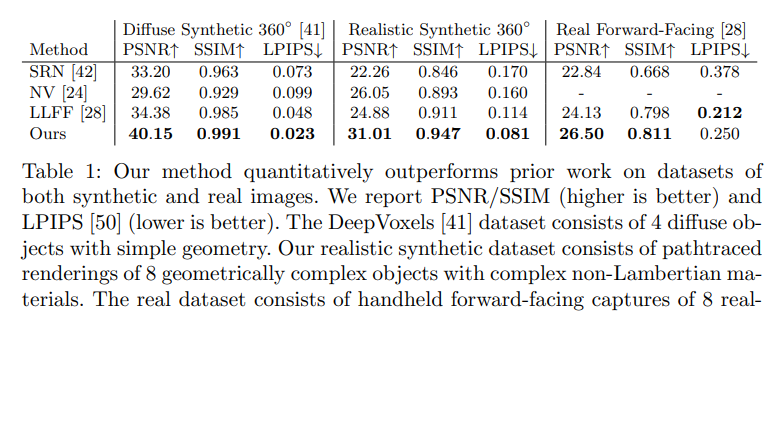
Results





Leave a comment